Calculator for the confidence interval of R squared (coefficient of determination).
Entirely free download of software

The correlation coefficient (R) is often represented by R squared, the coefficient of determination or explantion. This coefficient (between 0 and 1) is a measure for the goodness of fit of a regression line or curve. R=1 means a perfect fit while R=0 means zero fit. The calculator program gives the range over which the calculated R or R squared value may deviate from the true value. The range is determined by the assumed probability (confidence) interval.         Screenprint of the R-squared calculator: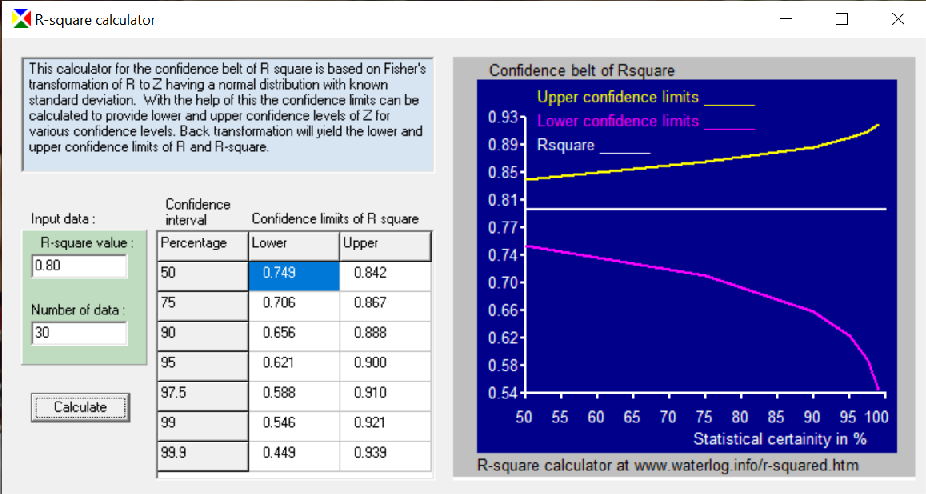

Download: R-squared calculator. Go to: software & models articles & manuals reports case studies FAQ's & papers home page

MATHEMATICS The confidence interval for R or R squared is based on the normal probability distribution. To use that distribution Fisher's transformation needs to be applied to R:         Z = 0.5 * ln [ (1-R) / (1+R) ] where Z is the transformed R value. Z has been proved to follow a normal distribtion with standard deviation (S) defined by:         S squared = 1/(N-3) where N is the number of data sets. With S, confidence intervals for Z can be found as follows:         ZL =  Z - F * S         ZU = Z + F * S where ZL is the lower confidence limit of Z, ZU is the upper confidence limit, and F is a factor dependeing on the degree of confidence desired: For 50% confidence F = 0.674 For 75% confidence F = 1.150 For 90% confidence F = 1.65 For 95% confidence F = 1.96 For 97.5% confidence F = 2.24 For 99% confidence F = 2.58 For 99.9% confidence F = 3.29 After finding ZL and ZU, these values must be transformed back to RL and RU, RL being the lower confidence limit of R and RU the upper confidence limit. We have:         RL = [exp(2*ZL)-1] / [exp(2*ZL) +1];         RU = [exp(2*ZU)-1] / [exp(2*ZU) +1]; The upper and lower confidence limits of R squared can now be found using the squared values of RL and RU.